Collinearity test

Test for linear or nonlinear collinearity/correlation in data

collinear(x, p = 0.85, nonlinear = FALSE, p.value = 0.001)

Arguments

x	A data.frame or matrix containing continuous data
p	The correlation cutoff (default is 0.85)
nonlinear	A boolean flag for calculating nonlinear correlations (FALSE/TRUE)
p.value	If nonlinear is TRUE, the p value to accept as the significance of the correlation

Value

Messages and a vector of correlated variables

Details

Evaluation of the pairwise linear correlated variables to remove is accomplished through calculating the mean correlations of each variable and selecting the variable with higher mean. If nonlinear = TRUE, pairwise nonlinear correlations are evaluated by fitting y as a semi-parametrically estimated function of x using a generalized additive model and testing whether or not that functional estimate is constant, which would indicate no relationship between y and x thus, avoiding potentially arbitrary decisions regarding the order in a polynomial regression.

Author

Jeffrey S. Evans <jeffrey_evans<at>tnc.org>

Examples

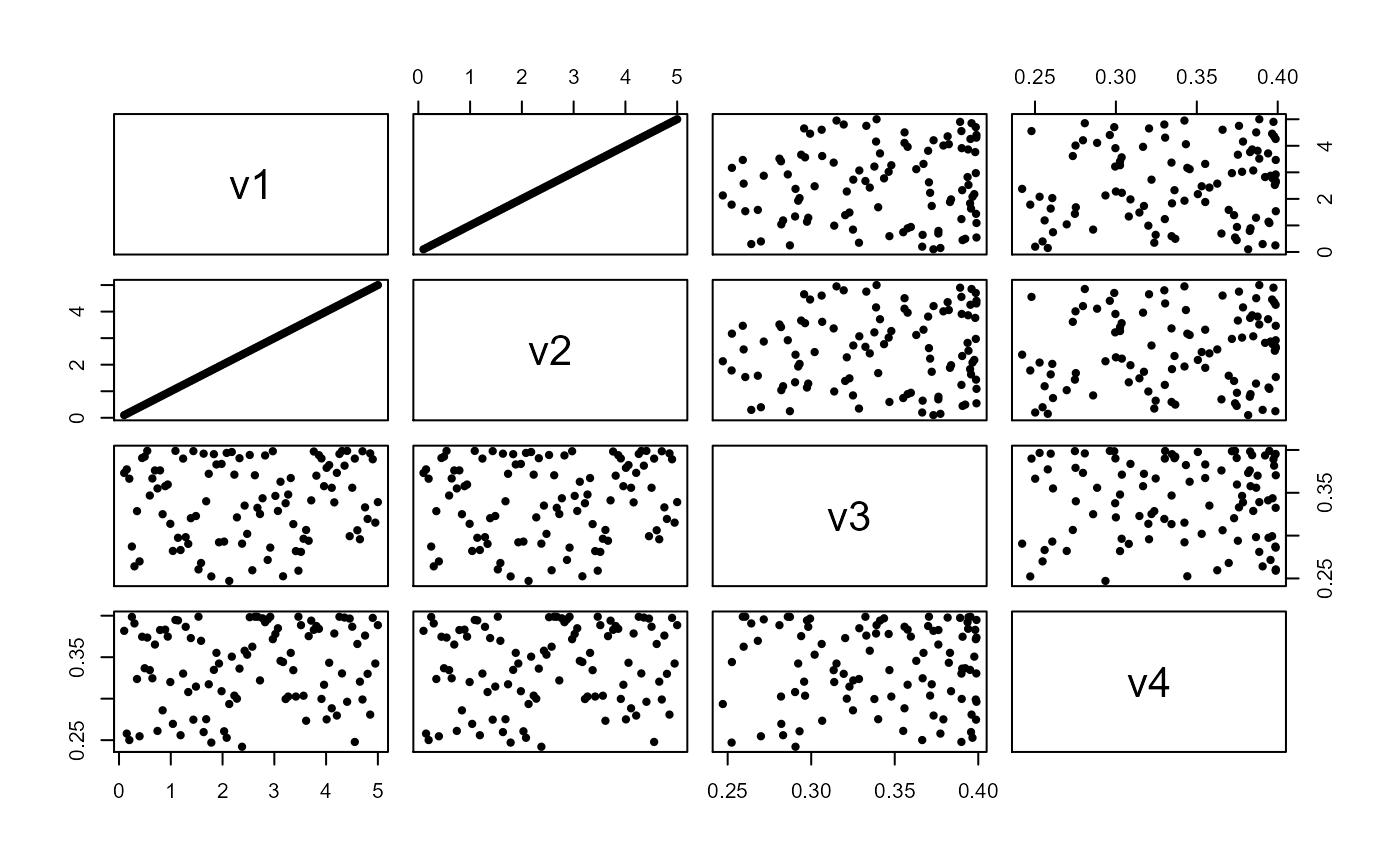
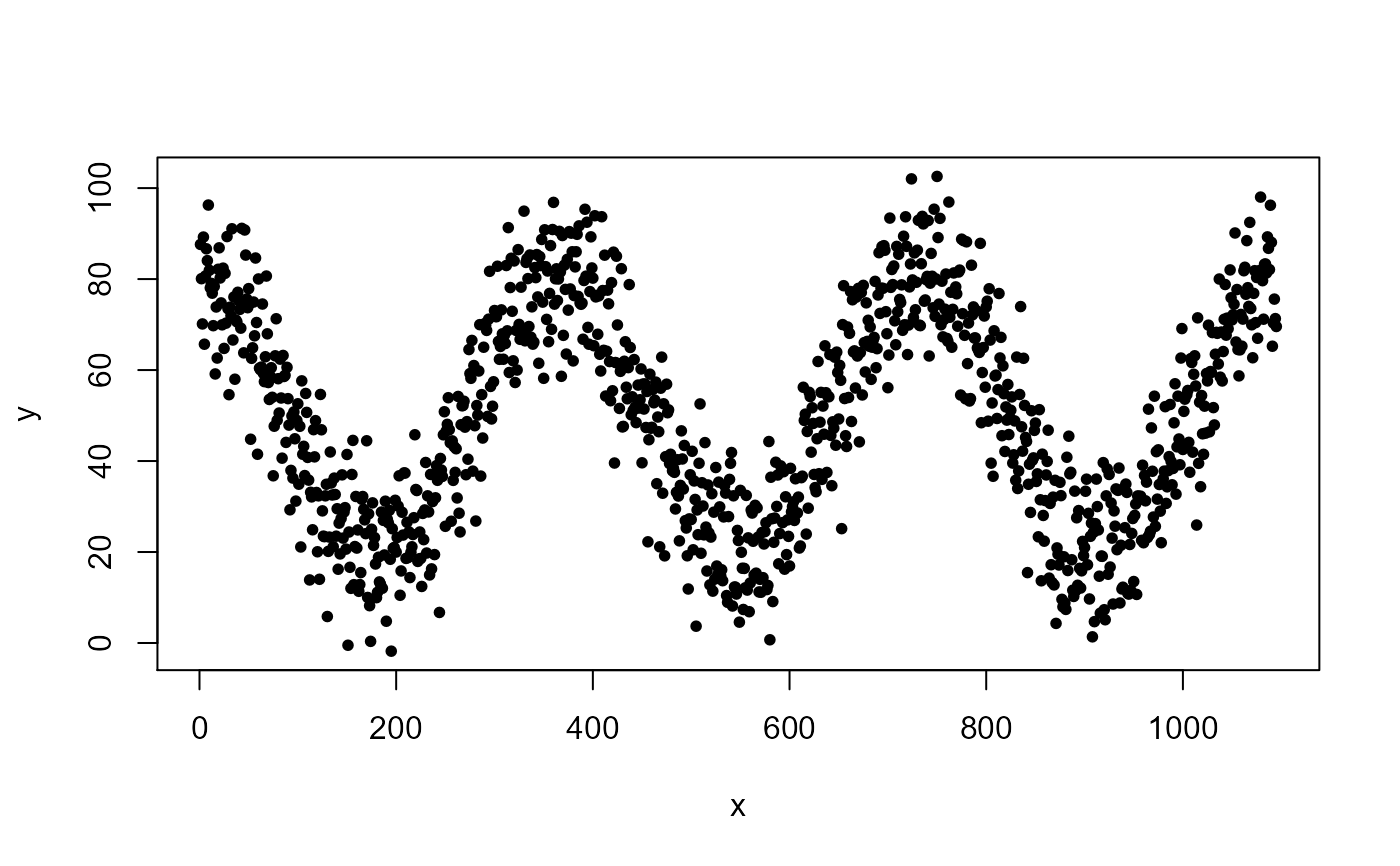
data(cor.data)

# Evaluate linear correlations on linear dataCollinearity between
head( dat <- cor.data[[4]] ) 
#>          v1        v2        v3        v4
#> 1 0.1000000 0.1000000 0.3731468 0.3817370
#> 2 0.1494949 0.1494949 0.3773337 0.2579079
#> 3 0.1989899 0.1989899 0.3664366 0.2501137
#> 4 0.2484848 0.2484848 0.2872536 0.3985506
#> 5 0.2979798 0.2979798 0.2641251 0.3906866
#> 6 0.3474747 0.3474747 0.3285911 0.3237098
pairs(dat, pch=20)
  ( cor.vars <- collinear( dat ) )
#> Collinearity between v1 and v2 correlation = 1
#>   Correlation means: 0.403 vs 0.182
#>    recommend dropping v1
#> 
#> [1] "v1"

# Remove identified variable(s)
head( dat[,-which(names(dat) %in% cor.vars)] )
#>          v2        v3        v4
#> 1 0.1000000 0.3731468 0.3817370
#> 2 0.1494949 0.3773337 0.2579079
#> 3 0.1989899 0.3664366 0.2501137
#> 4 0.2484848 0.2872536 0.3985506
#> 5 0.2979798 0.2641251 0.3906866
#> 6 0.3474747 0.3285911 0.3237098

# Evaluate linear correlations on nonlinear data
#   using nonlinear correlation function
plot(cor.data[[1]], pch=20) 
  collinear(cor.data[[1]], p=0.80, nonlinear = TRUE )            
#> evaluating y and x
#> Nonlinear correlation between y and x = 0.80918954845114
#>    recommend dropping x
#> 
#> evaluating x and y
#> [1] "x"